Regresi Logistik atau Logit di Stata

Regresi logistik merupakan regresi yang digunakan saat variabel dependennya adalah variabel biner (memiliki dua output). Umumnya kita ingin melihat berapa probabilitas variabel dependen bernilai tertentu jika variabel independen memiliki nilai tertentu. Regresi logistik berusaha memaksimalkan fungsi log likelihood berbeda dengan OLS yang akan meminimalkan sum squares of error.

Baca juga: cara-membaca-hasil-regresi-logistik-di-stata

Kita akan menggunakan data dari penerimaan mahasiswa yang mendaftar ke jurusan kedokteran di Amerika. Kamu bisa mendownload datanya di link dibawah

Variabel acceptance akan kita jadikan sebagai variabel dependen (yang dipengaruhi). Variabel seperti inilah yang kita sebut dengan variabel biner karena memiliki nilai antara 1 atau 0, bernilai 1 untuk diterima dan bernilai 0 untuk tidak diterima. Untuk itu regresi logistik dilakukan untuk melihat bagaimana perkiraan individu tersebut diterima atau tidak berdasarkan faktor faktor lain.

Perhatian: kita akan menggunakan standar umum di luar negeri dengan koma menjadi “.” untuk memudahkan translasi dari software

Ingat kembali bahwa probabilitas ≠ odds
Dimana odds memiliki hubungan identitas dengan probabilitas 
Odds = p/(1-p)

Sementara itu log odds hanyalah fungsi logaritma dari odds
Log odds = log (odds)
Odds = antilog (log odds) = e^{(log odds)} = exp (log odds)

Sementara itu logit adalah
logit(p) = log odds (p) =  log(odds(p))

Regresi logistik tanpa variabel independen

Mari kita mulai dengan model paling simpel dimana kita menjadikan variabel acceptance yang bernilai 1 jika diterima atau 0 jika tidak diterima sebagai satu satunya variabel dalam model. Untuk menjalankan regresi logistik kita akan menggunakan command logit dengan model sebagai berikut

logit(p) = β0

Dimana p adalah probabilitas acceptance bernilai 1

hasil logit dari model paling sederhana pertama kita akan seperti dibawah ini dengan command pada stata

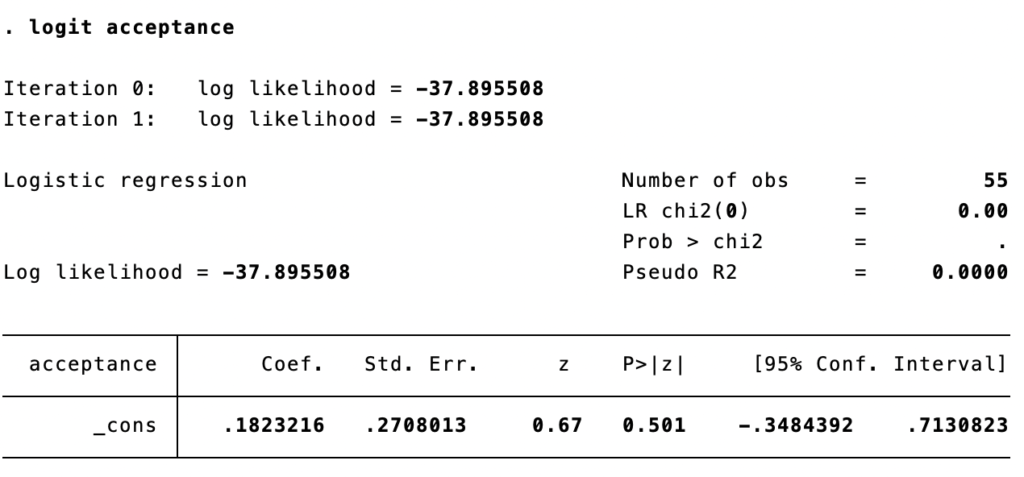
logit acceptance

kita juga akan memunculkan tabel frekuensi dengan command pada stata

tabulate acceptance

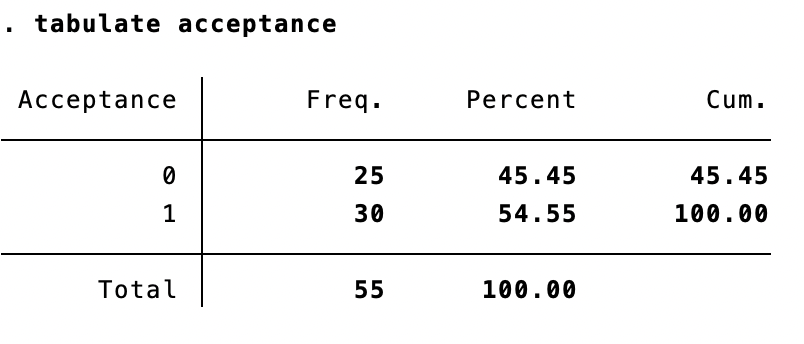
Dari tabel ini probabilitas acceptance bernilai 1 (p) = 30/55 = 0.5455. Odds nya adalah 0.5455/(1-0.5455) = 1.2 dan log odds (logit) adalah log(1,2) =  0.1823216. Dengan kata lain, intersep dari model tanpa variabel prediktor (independen) adalah perkiraan log odds diterima di universitas (acceptance=1) untuk seluruh populasi. 

Regresi logistik dengan variabel dummy/ kategori

Sekarang mari kita menambahkan variabel dummy/kategori pada model berupa variabel jenis kelamin (sex) dimana sex=1 jika laki-laki dan sex=0 jika perempuan

Sehingga model kita menjadi

logit(p) = β0 + β1 * sex

Sebelum itu mari kita menghitung odds dan odds ratio secara manual dengan tabel frekuensi silang sebagai berikut menggunakan command

tabulate acceptance sex

Dalam data yang kita gunakan odds laki laki (sex = 1) diterima di universitas (acceptance = 1) bila dihitung secara manual adalah 12/15 = 0.8. Sementara itu odds perempuan (sex = 0) diterima di universitas (acceptance = 1) adalah 18/10 = 1.8. Sehingga odds ratios bagi laki laki diterima di universitas dibanding perempuan adalah 0.8/1.8 = 0.44 atau dengan kata lain odds laki laki diterima di universitas adalah sebesar 0.44 kali dari perempuan atau dengan kata lain 55% lebih rendah daripada perempuan.

Mari kita lihat hasil regresi logistik melalui command stata

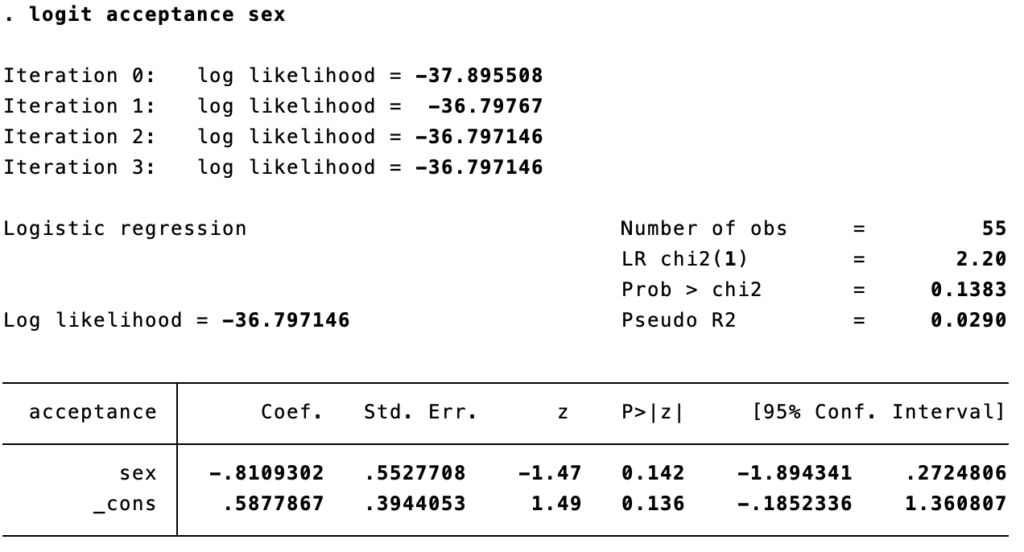
logit acceptance sex

Dengan hasil odds ratio sebagai berikut, dengan command stata

logit acceptance sex, or

Kebanyakan program statistik bisa langsung menampilkan hasil odds rationya seperti pada program stata yang kami gunakan. Di hasil pertama koefisien dari model dalam bentuk log odds sementara di hasil kedua koefisien dalam bentuk odds ratio. Kamu bisa mengujinya dengan mengubah koefisien dalam log odds menjadi odds (exp(-0.8109302) = 0.4444444)

Pada hasil pertama karena koefisien dalam bentuk log odds maka kita bisa menginterpretasikannya sebagai berikut. Bila siswa tersebut seorang laki laki (sex = 1) maka log odds ia diterima di universitas (acceptance = 1) akan  0.8109302 lebih rendah dibanding bila siswa tersebut perempuan (sex = 0)

Sementara itu hasil kedua yang koefisiennya dalam bentuk odds ratio dapat diinterpretasikan sebagai berikut. Bila siswa tersebut adalah seorang laki-laki (sex = 1) maka odds dia diterima di universitas akan menjadi 0.44444 kali lipat dibanding saat siswa tersebut seorang perempuan (sex = 0). Atau dengan kata lain saat ia laki laki, maka odds nya diterima di universitas 55% lebih rendah daripada perempuan.

Regresi logistik dengan variabel kontinu

Selanjutnya kita akan menambahkan satu variabel kontinu dalam model sederhana kita, kita akan menggunakan nilai GPA sebagai variabel independen dalam model, sehingga kita akan melihat pengaruh GPA dalam penerimaan ke universitas

logit(p) = β0 + β1 GPA

Kita bisa langsung menjalankan regresi logistik ini dengan command

logit acceptance gpa

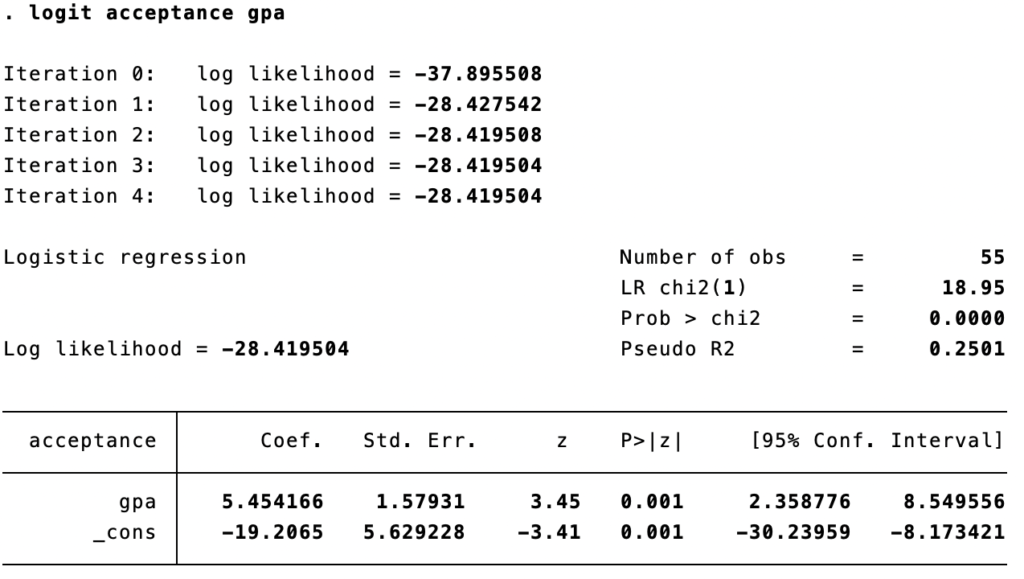
Dalam model ini, koefisien untuk intersep adalah log odds seorang siswa dengan GPA nol diterima di universitas. Dengan kata lain, probabilitas seseorang diterima di universitas dengan GPA adalah nol adalah exp(-19.2065) = 0.00000000455746176 atau dengan kata lain hampir tidak mungkin. Namun jika kita melihat distribusi dari GPA, kita akan melihat bahwa tidak ada seorang pun dalam sampel yang memiliki GPA lebih rendah dari 2.7

Bagaimana kita menafsirkan koefisien untuk variabel GPA? Model ini memberikan kita persamaan regresi sebagai berikut

logit(p; acceptance = 1) = -19.2065 + 5.454166 * GPA

Misalkan kita ingin melihat berapa kemungkinan siswa diterima saat memiliki nilai GPA sebesar 2,8

logit(p; GPA = 2.8) = -19.2065 + 5.454166 *  2.8 

Kita akan menghitungnya nanti, mari kita lihat bagaimana jika seorang siswa tersebut memiliki GPA sebesar 3.8

logit(p; GPA = 3.8) = -19.2065 + 5.454166 *  3.8 

Bila kita ingin melihat perbedaan dari hasil kedua persamaan tersebut maka

logit(p; GPA = 3.8) - logit(p; GPA = 2.8) = 5.454166

Sehingga dengan kata lain koefisien dari GPA adalah perbedaan log odds yang terjadi. Atau dengan kata lain saat GPA meningkat sebanyak 1 unit maka log odds akan meningkat sebesar koefisien

Koefisien ini bisa juga dikatakan sebagai log odds ratios, karena bersifat sebagai perbandingan. Mari kita lihat bagaimana koefisien log odds ini jika diubah menjadi odds

Ingat kembali bahwa 
Log odds = log (odds)
Odds = antilog (log odds) = e^{(log odds)} = exp (log odds)

Sehingga 
Odds = exp (5.454166) = 233.7298591

Sehingga dengan kata lain setiap ada peningkatan GPA sebesar 1 unit, maka odds siswa tersebut diterima akan menjadi 233.72 kali lipat dari sebelumnya atau. Dalam program statistik odds ratio ini juga langsung dapat dihitung oleh program, dengan command

logit acceptance gpa, or

Regresi logistik dengan banyak variabel

Mari kita lihat bagaimana jika kita menggunakan banyak variabel independen dalam mode, misalkan kita akan menggunakan variabel sex, gpa, BCPM dan apps, sehingga model kita menjadi

logit(p) = β0 + β1 sex +  β2 gpa + β3 apps 

Dimana 

Sex → jenis kelamin, bernilai 1 bila laki-laki dan 0 bila perempuan (variabel dummy)
Gpa → nilai GPA (variabel kontinu)
Apps → jumlah universitas yang di kirim aplikasi (variabel kontinu)

Dengan command stata 

logit acceptance sex gpa apps

Dengan hasil sebagai berikut

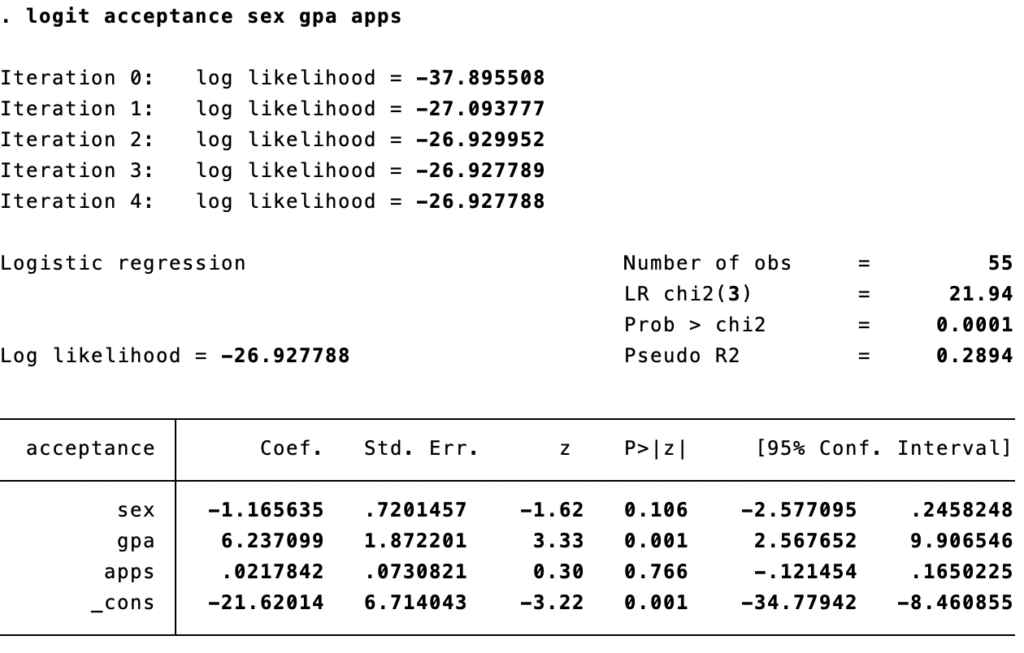
Interpretasi variabel masih sama dengan regresi sebelumnya, tinggal melihat apakah variabel tersebut merupakan variabel dummy atau kontinu