Cara Membaca Hasil Regresi Logistik di Stata

Artikel ini akan membahas cara membaca hasil regresi logistik di stata secara detail, bila kamu ingin melihat bagaimana cara menjalankan regresi logistik di stata kamu bisa melihatnya pada artikel berikut bisariset.id/regresi-logistik-atau-logit-di-stata/

Ingat kembali bahwa regresi logistik merupakan regresi yang digunakan saat variabel dependennya adalah variabel biner (memiliki dua output). Umumnya kita ingin melihat berapa probabilitas variabel dependen bernilai tertentu jika variabel independen memiliki nilai tertentu.  Regresi logistik berusaha memaksimalkan fungsi log likelihood (LL) berbeda dengan OLS yang akan meminimalkan sum squares of error.  

Kita akan menggunakan data penerimaan mahasiswa kedokteran di Amerika dengan model sebagai berikut

logit(p) = β0 + β1 sex +  β2 gpa + β3 apps 

Dimana 
p → probabilitas acceptance bernilai 1, 1=diterima; 0=ditolak (variabel dummy/biner)
sex → jenis kelamin, bernilai 1 bila laki-laki dan 0 bila perempuan (variabel dummy)
gpa → nilai GPA (variabel kontinu)
apps → jumlah universitas yang di kirim aplikasi (variabel kontinu)

Jika dilakukan regresi logistik maka akan muncul hasil sebagai berikut

Dalam regresi logistik di stata umumnya akan terdapat 3 bagian utama yaitu iterasi log, ringkasan model dan estimasi parameter. Kita akan membahasnya secara detail satu per satu.

Iterasi log

Iterasi log merupakan daftar kemungkinan nilai log likelihood pada setiap iterasi. Ingat kembali bahwa regresi logistik menggunakan maximum likelihood yang ingin memaksimalkan nilai dari log likelihood (terlihat dari setiap iterasi mengalami peningkatan log likelihood sampai estimasi terakhir), yang merupakan prosedur berulang. 

Iterasi pertama ( iterasi 0) adalah nilai log likelihood (LL) dari model “null” atau “kosong”; yaitu, model tanpa prediktor (kamu bisa mendapatkan nilai ini hanya dengan meregresikan logistik variabel dependen saja). 

Pada iterasi berikutnya, prediktor (variabel independen) dimasukkan ke dalam model. Pada setiap iterasi, nilai log likelihood meningkat karena tujuannya adalah untuk memaksimalkan nilai log likelihood. Ketika perbedaan antara iterasi yang berurutan sangat kecil (dalam contoh ini terjadi pada iterasi 4), model dikatakan telah “konvergen”, iterasi dihentikan dan hasilnya ditampilkan.

Ringkasan model

Log likelihood → nilai terakhir dan maksimum dari iterasi log likelihood. Nilai -26.927788 tidak memiliki arti secara langsung namun akan digunakan dalam perhitungan lainnya

Number of obs → jumlah pengamatan (data) yang digunakan dalam analisis. Jumlah ini mungkin lebih kecil dari jumlah total pengamatan dalam kumpulan data jika memiliki nilai yang hilang (kosong) untuk salah satu variabel yang digunakan dalam regresi logistik. Stata menggunakan penghapusan listwise secara default, yang berarti bahwa jika ada nilai yang hilang untuk variabel apa pun dalam regresi logistik, seluruh data subjek akan dikeluarkan dari analisis.

LR chi2(3) → nilai uji chi-square likelihood ratio (LR). Chi-square likelihood ratio dapat dihitung dengan manual sebagai 2*( -37.895508 (nilai iterasi 0) – -26.927788 (nilai iterasi terakhir) ) = 21.93544. Angka dalam kurung menunjukkan degree of freedom. Dalam model ini, ada tiga prediktor (variabel independen), jadi ada tiga  degree of freedom.

Prob > chi2 → Probabilitas untuk memperoleh chi-square dengan anggapan hipotesis nol benar (tidak ada hubungan variabel independen terhadap dependen). Nilai-p umumnya dibandingkan dengan nilai kritis, mungkin 0.05 atau 0.01 untuk menentukan apakah model keseluruhan signifikan secara statistik. Dalam kasus ini, model signifikan secara statistik karena nilai p kurang dari .01

Pseudo R2 → nilai pseudo R² MacFadden, regresi logistik tidak dapat menghitung nilai R² dengan arti sama pada OLS (proporsi varians dijelaskan oleh model) sehingga dibuatlah padanannya. Dalam stata metode yang digunakan adalah MacFadden pseudo R² yang secara manual dapat dihitung dengan (LL iterasi pertama – LL iterasi terakhir)/ LL iterasi pertama dimana LL menjadi padanan varians di OLS. Bila dihitung maka  (-37.895508 – -26.927788)/ -37.895508 = 0.28942005. Sehingga pseudo R² MacFadden dapat diartikan sebagai proporsi log likelihood yang dijelaskan oleh model

Estimasi parameter

acceptance → variabel biner dependen dalam model, variabel dibawahnya merupakan variabel independen dan _cons adalah nilai konstanta

coef. → nilai koefisien untuk persamaan regresi logistik untuk memprediksi variabel dependen dari variabel independen. Nilai koefisien ini dalam log odds. Mirip dengan regresi OLS, persamaan prediksinya adalah

logit(p) = log (odds(p)) = log (p/(1-p) = β0 + β1 sex +  β2 gpa + β3 apps 
logit(p) = -21.62014 + -1.165365(sex) + 6.237099(gpa) + 0.0217842(apps)

sex – nilai koefisien sex adalah -1.165365, ini berarti bila sex bernilai 1 (laki-laki) maka log odds dari p (acceptance bernilai 1, atau diterima) lebih rendah sebesar 1.165365 bila dibandingkan sex bernilai 0 (perempuan). Kita membandingkan sex bernilai 1 dan 0 karena sex merupakan variabel dummy
gpa – nilai koefisien gpa adalah 6.237099, ini berarti bila gpa meningkat sebanyak 1 unit, maka log odds diterima akan meningkat sebanyak  6.237099
apps – nilai koefisien apps adalah 0.0217842, ini berarti bila apps meningkat sebanyak 1 unit, maka log odds diterima akan meningkat sebanyak  0.0217842
_const – nilai konstanta adalah -21.62014, ini berarti bila semua variabel independen lain bernilai 0, maka log odds diterima akan sebesar 21.62014

Ingat kembali bahwa odds, log odds dan probabilitas merupakan konsep yang berbeda. Untuk detailnya kamu bisa membaca artikel berikut bisariset.id/odds-log-odds-dan-odds-ratio/

Std. Err. → nilai standar error yang berkaitan dengan koefisien. Standar error digunakan untuk menguji apakah nilai parameter secara signifikan berbeda dari 0. Dengan membagi estimasi parameter (koefisien) dengan standar error, kita akan mendapatkan nilai-z. Standar error juga akan digunakan untuk membentuk interval kepercayaan untuk koefisien, seperti pada dua kolom terakhir dari tabel.

Z → nilai z pada distribusi normal, didapatkan dengan membagi koefisien dengan standar error

P>|z| → nilai P value dua sisi (two-tailed) dari nilai z, kita akan melihat nilai ini untuk melihat apakah variabel independen secara signifikan mempengaruhi variabel dependen. Umumnya kita akan menggunakan tingkat signifikansi 0.1, 0.05 dan 0.01, bila nilainya dibawah tingkat signifikansi yang kita pilih maka dapat dikatakan variabel independen tersebut signifikan mempengaruhi variabel dependen. Sebagai contoh kita akan menggunakan tingkat signifikansi 0.05, gpa memiliki nilai p sebesar 0.001 sehingga dapat dikatakan variabel gpa signifikan mempengaruhi acceptance karena nilai p valuenya lebih rendah dari 0.05. Sementara itu apps dengan nilai p 0.766 tidak signifikan mempengaruhi variabel dependen karena nilai p nya lebih besar dari 0.05.

[95% Conf. Interval] → menunjukkan nilai interval kepercayaan 95% untuk koefisien. Nilai ini digunakan untuk memahami seberapa tinggi dan seberapa rendah nilai populasi sebenarnya dari koefisien tersebut.

Membaca hasil odds ratios

Dalam regresi logistik kita juga bisa menampilkan estimasi parameter (koefisien) dalam bentuk odds ratios dengan command logistic maupun penambahan or dibelakang command logit. Hasilnya akan sebagai berikut

Komponen yang dihasilkan masih sama dengan sebelumnya, yang berbeda hanyalah nilai koefisien dalam odds ratio. Ingat kembali bahwa untuk mengubah nilai log odds menjadi odds ratio kita hanya perlu melakukan antilog, sehingga 

Odds = antilog (log odds) = e(log odds) = exp (log odds)

Dimana odds ratio adalah rasio dari odds

Mari kita interpretasikan nilai koefisien dalam odds ratio ini

sex – nilai koefisien odds ratio sex adalah 0.3117247, ini berarti bila sex bernilai 1 (laki-laki) maka odds dari (acceptance bernilai 1, atau diterima) akan menjadi  0.3117247 kali lipat dari odds saat sex bernilai 0 (perempuan). Misal odds bagi sex=0 (perempuan) diterima di universitas adalah 2, maka odds bagi sex=1 (laki laki) adalah 0.3117247 kalinya, atau sebesar 0.3117247*2 = 0.6234494
gpa – nilai koefisien odds ratio gpa adalah 511.3727, ini berarti bila gpa meningkat sebanyak 1 unit, maka odds diterima akan menjadi 511.3727 kali lipat dari sebelumnya
apps – nilai koefisien odds ratio apps adalah 1.022023, ini berarti bila apps meningkat sebanyak 1 unit, maka odds diterima akan menjadi 1.022023 kali lipat dari sebelumnya
_const – nilai konstanta adalah  4.08e-10, ini berarti bila semua variabel independen lain bernilai 0, maka odds diterima akan sebesar 4.08e-10

Membaca hasil marginal effect pada regresi logistik

Dalam regresi logistik kita juga seringkali akan menjumpai hasil dari marginal effectnya, umumnya marginal effect ini adalah hasil yang sering dijumpai mendampingi hasil koefisien dalam log odds dan odds ratio karena dapat langsung diinterpretasikan sebagai nilai probabilitas. Berikut adalah hasil marginal effect pada model sebelumnya, ingat kembali bahwa regresi logistik menggunakan fungsi non linier sehingga marginal effect yang digunakan adalah average marginal effect

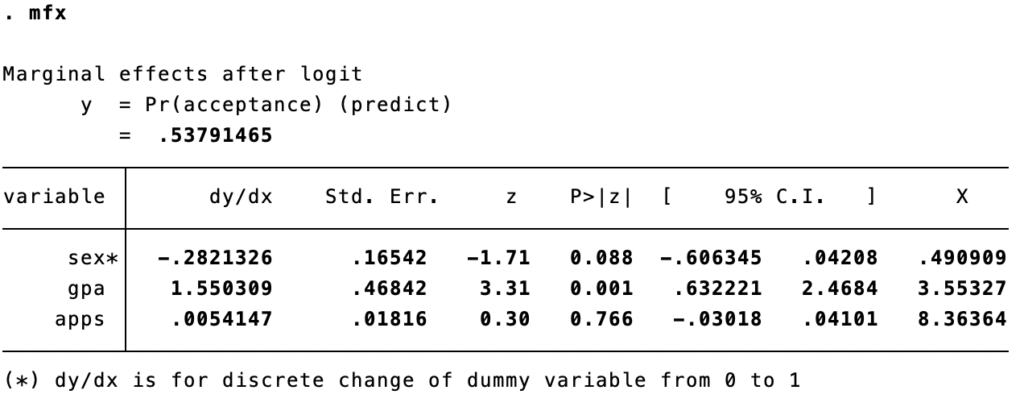
sex → nilai dy/dx sex adalah -0.282, ini berarti probabilitas diterima (acceptance=1) bila laki-laki (sex=1) akan 0.282 atau 28.2% lebih rendah daripada bila subjek perempuan (sex=0)
gpa → nilai dy/dx gpa adalah 1.55, ini berarti bila gpa meningkat sebanyak 0.1 unit maka probabilitas diterima (acceptance=1) akan meningkat sebesar 0.155 atau 15.5%
apps → nilai dy/dx apps adalah .005, ini berarti bila apps meningkat sebanyak 1 unit maka probabilitas diterima (acceptance=1) akan meningkat sebesar .005 atau 0.5%