Multikolinearitas adalah masalah umum dalam analisis regresi, di mana dua atau lebih variabel independen berkorelasi tinggi satu sama lain. Hal ini dapat menyebabkan estimasi koefisien regresi yang tidak akurat, standar kesalahan yang terlalu tinggi, dan daya statistik yang berkurang. Untuk menentukan apakah masalah multikolinearitas terjadi, kita dapat melakukan uji multikolinearitas, yang dibahas dalam artikel ini.
Apa itu Multikolinearitas
Multikolinearitas terjadi ketika terdapat hubungan linier atau korelasi yang tinggi antara dua atau lebih variabel independen dalam model regresi. Hal ini berarti bahwa satu variabel independen dapat diprediksi dari variabel independen lainnya dengan tingkat akurasi yang tinggi.
Sebagai contoh, misalkan kita ingin mempelajari efek pendidikan dan pendapatan terhadap kepuasan hidup. Kita mengumpulkan data dari sampel individu dan menyesuaikan model regresi linier:
kepuasan_hidup = b0 + b1 * pendidikan + b2 * pendapatan + error
Namun, kita menemukan bahwa pendidikan dan pendapatan berkorelasi tinggi satu sama lain, artinya orang dengan pendidikan tinggi cenderung memiliki pendapatan yang tinggi juga. Ini menciptakan masalah multikolinearitas, karena sulit untuk memisahkan efek individu pendidikan dan pendapatan terhadap kepuasan hidup.
Mengapa Multikolinearitas Menjadi Masalah
Multikolinearitas dapat menyebabkan masalah pada model regresi, seperti halnya:
- Koefisien regresi dapat menjadi tidak stabil dan sensitif terhadap perubahan kecil dalam data atau spesifikasi model. Ini berarti bahwa koefisien dapat berubah drastis tergantung pada variabel mana yang dimasukkan atau dikecualikan dari model, atau bagaimana data diambil sampel atau diukur.
- Standar kesalahan koefisien regresi dapat menjadi terlalu tinggi, mengarah pada interval kepercayaan yang lebih lebar dan uji-t yang kurang signifikan. Ini berarti bahwa kita mungkin gagal menolak hipotesis nol tidak ada efek ketika sebenarnya ada efek, atau sebaliknya.
- Kesesuaian keseluruhan model dapat berkurang, seperti yang diukur oleh R-squared atau adjusted R-squared. Ini berarti bahwa model mungkin tidak menjelaskan banyak variasi dalam variabel dependen, meskipun memiliki banyak variabel independen.
- Interpretasi koefisien regresi dapat menjadi ambigu atau menyesatkan. Ini berarti bahwa kita mungkin tidak dapat mengatakan variabel independen mana yang memiliki efek lebih kuat atau lebih lemah pada variabel dependen, atau apakah efeknya positif atau negatif.
Cara Melakukan Uji Multikolinearitas
Untuk mendeteksi multikolinearitas dalam model regresi, terdapat beberapa cara yang dapat dilakukan dengan menjalankan beberapa tes yang sudah tersedia, yaitu:
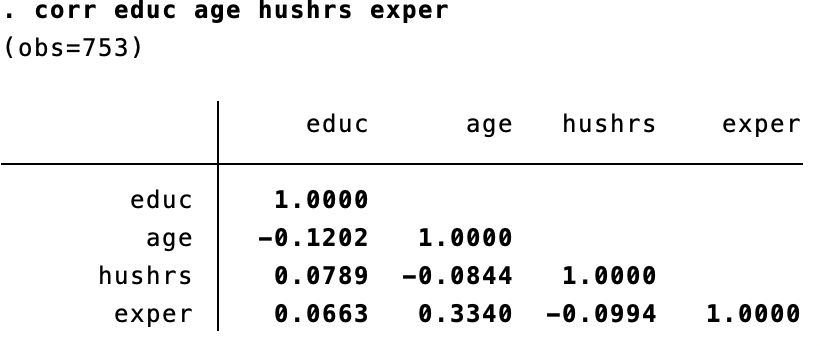
- Mengamati matriks korelasi variabel independen. Korelasi yang tinggi (di atas 0,8 atau di bawah -0,8) antara dua atau lebih variabel independen menunjukkan masalah potensial multikolinearitas.
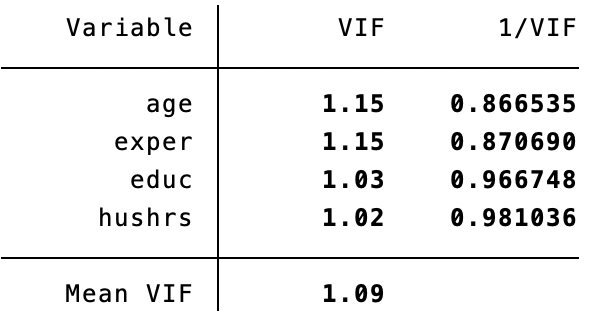
- Menghitung faktor inflasi varian (VIF) untuk setiap variabel independen. VIF mengukur seberapa banyak variansi koefisien regresi terpengaruh oleh multikolinearitas. VIF di atas 10 (atau di atas 5 menurut beberapa sumber) menunjukkan masalah serius multikolinearitas.
- Melakukan dekomposisi eigenvalue dari matriks variabel independen. Eigenvalue mewakili jumlah varians yang dijelaskan oleh setiap kombinasi linear variabel independen. Eigenvalue yang sangat kecil (dekat dengan nol) menunjukkan tingkat multikolinearitas yang tinggi antara beberapa variabel independen.
Cara Menangani Multikolinearitas
Jika multikolinearitas terdeteksi, ada beberapa cara untuk menangani masalah tersebut, seperti:
- Mengeluarkan salah satu variabel yang berkorelasi. Jika dua atau lebih variabel independen berkorelasi tinggi, kita dapat mengeluarkan salah satunya dari model. Ini dapat dilakukan dengan memeriksa nilai VIF atau toleransi untuk menentukan variabel mana yang paling berkontribusi pada multikolinearitas.
- Menggabungkan variabel yang berkorelasi. Jika dua atau lebih variabel independen berkorelasi tinggi, kita dapat menggabungkannya menjadi satu variabel. Ini dapat dilakukan dengan membuat variabel baru yang merupakan jumlah atau rata-rata dari variabel yang berkorelasi.
- Menggunakan metode regresi yang berbeda. Beberapa metode regresi, seperti ridge regression and elastic net regression, lebih kuat terhadap multikolinearitas daripada regresi biasa (Ordinary Least Squares/OLS).
Penting untuk dicatat bahwa multikolinearitas tidak selalu menjadi masalah. Dalam beberapa kasus, mungkin sepenuhnya dapat diterima memiliki dua atau lebih variabel independen yang berkorelasi tinggi. Namun, penting untuk menyadari masalah potensial yang dapat ditimbulkan oleh multikolinearitas dan mengambil langkah-langkah untuk mengatasinya jika diperlukan.


