Distribusi normal adalah salah satu konsep paling penting dalam statistik. Ini menggambarkan bagaimana nilai variabel kontinu didistribusikan di sekitar rata-rata dan deviasi standar. Dalam posting blog ini, kami akan menjelajahi beberapa properti dan aplikasi distribusi normal, dan bagaimana menggunakannya untuk menganalisis data.????????
Distribusi normal, juga dikenal sebagai distribusi Gaussian, adalah distribusi probabilitas kontinu yang mendasar. Ini simetris di sekitar mean dan menghasilkan kurva berbentuk lonceng ketika digrafikkan. Kurva berbentuk lonceng (bell curve) ini digunakan dalam banyak analisis statistik untuk mewakili fenomena yang berbeda dan merupakan konsep penting yang dipelajari dalam statistik.
Sifat Distribusi Normal
Distribusi normal memiliki beberapa sifat penting yang biasanya digunakan dalam analisis statistik. Misalnya:
- Mean, median, dan mode bernilai sama. Ini berarti bahwa nilai yang paling sering muncul dalam distribusi juga merupakan nilai rata-rata, dan distribusi simetris di sekitar mean.
- Distribusi ini asimtotik. Ini berarti bahwa ekor distribusi meluas secara tak terhingga, tetapi mereka mendekati nol saat nilai menjadi sangat besar atau sangat kecil.
- Luas di bawah kurva sama dengan 1. Ini berarti bahwa semua nilai yang mungkin dari distribusi dihitung.
- Distribusi ini didefinisikan oleh dua parameter: mean dan simpangan baku. Mean menentukan pusat distribusi, dan simpangan baku menentukan lebar distribusi.
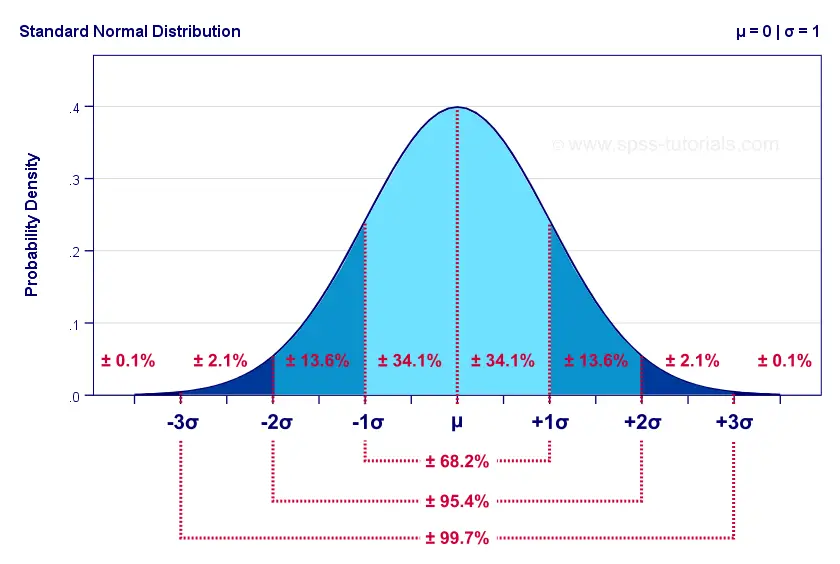
Pada data yang terdistribusi secara normal, sekitar 68% nilai berada dalam satu standar deviasi dari mean, 95% berada dalam dua standar deviasi, dan 99,7% berada dalam tiga standar deviasi. Hal ini dikenal sebagai aturan 68-95-99.7 atau aturan empiris. Berikut beberapa contoh data dunia nyata yang mengikuti distribusi normal:
- Skor IQ. Skor IQ juga terdistribusi secara normal, dengan mean 100 dan standar deviasi 15. Ini berarti bahwa sebagian besar orang memiliki skor IQ antara 85 dan 115, dan sejumlah kecil orang memiliki skor IQ yang jauh lebih rendah atau lebih tinggi.
- Skor tes. Skor pada tes standar, seperti nilai Ujian Nasional (UN) dan UTBK, juga terdistribusi secara normal. Ini berarti bahwa sebagian besar siswa mendapatkan skor dalam beberapa poin dari skor rata-rata, dan sejumlah kecil siswa mendapatkan skor yang jauh lebih tinggi atau lebih rendah.
- Kesalahan pengukuran. Ketika Anda mengukur sesuatu, selalu ada kesalahan dalam pengukuran tersebut. Kesalahan ini sering terdistribusi secara normal, artinya sebagian besar kesalahan kecil, dan sejumlah kecil kesalahan besar.
Aplikasi
Distribusi normal memiliki banyak aplikasi dalam berbagai bidang seperti keuangan, teknik, dan statistik. Misalnya:
- Mengestimasi parameter populasi: Distribusi normal dapat digunakan untuk mengestimasi mean dan simpangan baku populasi dari sampel. Hal ini dilakukan dengan menggunakan mean dan simpangan baku sampel untuk menghitung z-score untuk data. Z-score tersebut kemudian dapat digunakan untuk mencari probabilitas bahwa titik data tertentu akan muncul di populasi.
- Menguji hipotesis: Distribusi normal dapat digunakan untuk menguji hipotesis tentang parameter populasi. Misalnya, Anda dapat menggunakan distribusi normal untuk menguji hipotesis bahwa mean populasi sama dengan nilai tertentu.
- Membangun interval kepercayaan: Distribusi normal dapat digunakan untuk membangun interval kepercayaan untuk parameter populasi. Interval kepercayaan adalah rentang nilai yang mungkin mengandung parameter populasi yang sebenarnya. Interval kepercayaan dihitung dengan menggunakan mean sampel, simpangan baku, dan tingkat kepercayaan yang diinginkan.
- Kontrol kualitas: Banyak proses manufaktur mengikuti distribusi normal, dan perusahaan dapat menggunakan teknik kontrol proses statistik untuk memantau kualitas produk mereka. Misalnya, jika sebuah perusahaan memproduksi widget, mereka mungkin akan menggunakan distribusi normal untuk menentukan batas kendali atas dan bawah untuk berat widget. Jika berat widget di luar batas kendali tersebut, maka dianggap sebagai cacat.
- Diagnostik medis: Distribusi normal sering digunakan dalam diagnostik medis untuk menentukan probabilitas seseorang memiliki penyakit tertentu. Misalnya, jika tes darah untuk suatu penyakit memiliki distribusi normal, dokter dapat menggunakan hasil tes untuk menghitung probabilitas bahwa pasien memiliki penyakit tersebut.
Cara menguji apakah suatu data berdistribusi normal
Ada beberapa cara untuk menguji distribusi normal. Berikut beberapa metode yang paling umum:
Baca juga: Uji Normalitas – Bisa Riset
- Metode grafis: Metode ini melibatkan plotting data dengan cara yang dapat membantu Anda secara visual menilai apakah data terdistribusi normal. Beberapa metode grafis umum meliputi:
- Histogram: Histogram adalah grafik batang yang menunjukkan distribusi data dalam satu set. Jika data terdistribusi normal, histogram akan berbentuk lonceng.
- Box plot: Box plot adalah ringkasan grafis dari distribusi data yang menunjukkan nilai minimum, kuartil pertama, median, kuartil ketiga, dan nilai maksimum. Jika data terdistribusi normal, box plot akan simetris.
- Q-Q plot: Q-Q plot adalah perbandingan grafis dari kuantil data dengan kuantil distribusi normal. Jika data terdistribusi normal, titik pada Q-Q plot akan jatuh pada garis lurus.
- Tes statistik: Metode ini menggunakan rumus statistik untuk menghitung probabilitas bahwa data diambil dari distribusi normal. Beberapa tes statistik umum untuk distribusi normal meliputi:
- Uji Kolmogorov-Smirnov: Uji ini menghitung jarak maksimum antara fungsi distribusi empiris data dan fungsi distribusi kumulatif dari distribusi normal.
- Uji Shapiro-Wilk: Uji ini menghitung statistik yang mengukur deviasi data dari distribusi normal.
- Uji Anderson-Darling: Uji ini mirip dengan uji Shapiro-Wilk, tetapi lebih kuat.


