Analisis regresi berganda merupakan metode statistik yang kuat untuk mempelajari hubungan antara variabel dependen dan satu atau lebih variabel independen. Namun, sebelum menerapkan analisis regresi, beberapa asumsi harus dipenuhi untuk memastikan bahwa hasilnya dapat diandalkan dan akurat. Asumsi-asumsi ini dikenal sebagai uji asumsi klasik regresi.
Uji asumsi klasik regresi adalah uji awal yang perlu dilakukan untuk memastikan bahwa data kita memenuhi asumsi regresi. Uji ini dilakukan untuk memastikan bahwa model regresi menghasilkan hasil yang akurat dan dapat diandalkan. Ada enam asumsi umum yang harus dipenuhi:
- Linearitas: Hubungan antara variabel dependen dan independen bersifat linear.
- Normalitas residual: Residual analisis regresi terdistribusi secara normal.
- Homoskedastisitas: Variansi residual konstan di semua tingkat variabel independen.
- Independensi: Residual analisis regresi independen satu sama lain.
- Tidak ada multikolinearitas: Tidak ada korelasi tinggi antar variabel independen.
- Tidak ada autokorelasi (untuk data deret waktu): Tidak ada korelasi antara residual analisis regresi.
Linearitas
Asumsi pertama adalah linearitas, yang mengharuskan hubungan antara variabel dependen dan independen bersifat linear. Dalam kata lain, perubahan pada variabel dependen proporsional terhadap perubahan pada variabel independen. Asumsi ini penting karena jika dilanggar, hasil analisis regresi mungkin tidak akurat.
Salah satu cara untuk memeriksa linearitas adalah dengan menggunakan scatterplot, yang menampilkan secara grafis hubungan antara dua variabel. Di bawah ini adalah contoh scatterplot linear dan non-linear, kita dapat langsung melihat bahwa scatterplot kanan tidak linear, tetapi kuadratik.
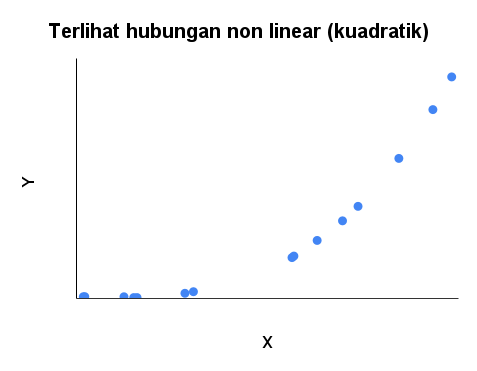
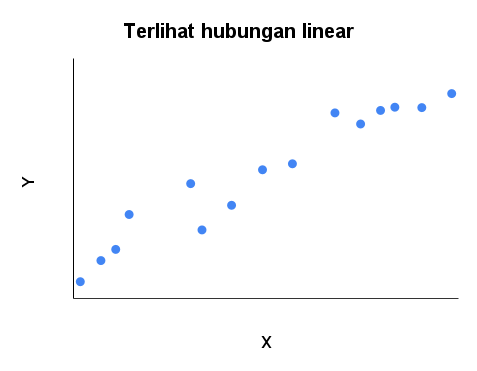
Jika linearitas dilanggar, ada beberapa teknik yang dapat digunakan untuk menangani asumsi tersebut. Salah satu teknik adalah dengan mentransformasi data, seperti termasuk kuadrat atau kubik, untuk membuat hubungan lebih linear. Teknik lainnya adalah dengan memperkenalkan interaksi variabel, yang memungkinkan adanya hubungan non-linear antara variabel. Regresi non-parametrik juga dapat digunakan untuk menangani hubungan non-linear antar variabel.
Normalitas Residual
Asumsi kedua dalam analisis regresi adalah normalitas residual. Ini berarti bahwa residual harus memiliki distribusi normal. Residual dihitung sebagai selisih antara nilai prediksi dan nilai aktual dari variabel dependen. Jika residual tidak mengikuti distribusi normal, maka dapat menyebabkan estimasi bias, inferensi yang salah, dan prediksi yang buruk.
Untuk memeriksa apakah residual terdistribusi normal, kita dapat menggunakan beberapa metode seperti normal probability plot, histogram, atau uji Shapiro-Wilk.
Jika normalitas tidak terpenuhi, mungkin diperlukan teknik transformasi seperti transformasi Box-Cox atau model regresi non-parametrik untuk menangani asumsi tersebut. Penting untuk dicatat bahwa penanganan asumsi normalitas harus dilakukan dengan hati-hati agar tidak memperkenalkan bias atau inferensi yang salah. Oleh karena itu, perlu menggunakan kombinasi metode yang berbeda untuk memastikan bahwa asumsi analisis regresi terpenuhi.
Homoskedastisitas
Asumsi ketiga dalam analisis regresi linear adalah homoskedastisitas, yang menetapkan bahwa variansi residual harus konstan di semua tingkat variabel independen. Hal ini penting karena memastikan bahwa kesalahan didistribusikan secara acak, dan bahwa koefisien regresi tidak bias dan efisien.
Jika asumsi ini dilanggar, dapat menyebabkan estimasi bias, inferensi yang salah, dan prediksi yang buruk. Oleh karena itu, penting untuk memeriksa homoskedastisitas sebelum membuat kesimpulan dari analisis regresi. Kita dapat memeriksa homoskedastisitas dengan menggunakan plot residual atau dengan melakukan uji Breusch-Pagan.
Jika homoskedastisitas ditemukan melanggar, ada beberapa teknik yang dapat digunakan untuk menangani asumsi tersebut. Salah satu teknik umum adalah dengan mentransformasi data, seperti mengambil logaritma, akar kuadrat, atau reciprok dari variabel. Pendekatan lain adalah dengan menggunakan regresi kuadrat terkecil yang tertimbang, yang memberikan lebih banyak bobot pada observasi dengan varians yang lebih kecil. Akhirnya, teknik regresi robust dapat digunakan untuk memperkirakan koefisien regresi yang kurang sensitif terhadap outlier dan pelanggaran asumsi homoskedastisitas.
Independensi Error
Asumsi keempat dalam analisis regresi adalah independensi error. Ini berarti bahwa residual, atau selisih antara nilai aktual dan nilai prediksi, harus independen satu sama lain. Dalam kata lain, kesalahan pada satu observasi tidak boleh berkaitan dengan kesalahan pada observasi lain.
Asumsi independensi error penting karena pelanggaran asumsi ini dapat menyebabkan estimasi bias, inferensi yang salah, dan prediksi yang buruk. Misalnya, jika terdapat pola pada residual, seperti tren naik atau turun, ini dapat menunjukkan bahwa ada hubungan antara kesalahan. Hal ini melanggar asumsi independensi dan dapat menyebabkan hasil yang tidak akurat.
Untuk memeriksa independensi error, terdapat beberapa metode yang tersedia. Salah satu cara adalah dengan menggunakan plot residual, yang dapat membantu memvisualisasikan pola atau tren pada residual. Cara lain adalah dengan menggunakan uji statistik seperti uji Durbin-Watson, yang menguji autokorelasi pada residual.
Jika independensi error dilanggar, ada beberapa teknik yang dapat digunakan untuk menangani asumsi tersebut. Misalnya, analisis deret waktu dapat digunakan ketika ada ketergantungan temporal antara kesalahan. Regresi kuadrat terkecil yang umum juga dapat digunakan untuk memperhitungkan korelasi antara kesalahan. Penting untuk menangani pelanggaran asumsi independensi error untuk memastikan validitas hasil analisis regresi.
Tidak Ada Multikolinearitas
Salah satu asumsi penting dalam analisis regresi adalah tidak adanya multikolinearitas, yaitu korelasi tinggi antara variabel independen yang dapat menyebabkan estimasi bias, inferensi yang salah, dan prediksi yang buruk. Untuk memeriksa multikolinearitas, kita dapat menggunakan matriks korelasi atau faktor inflasi varians.
Jika terdeteksi adanya multikolinearitas, maka perlu diambil tindakan korektif untuk menangani masalah tersebut. Salah satu solusi yang dapat dilakukan adalah dengan menggunakan analisis komponen utama untuk mengurangi dimensi data dengan menggabungkan variabel yang sangat berkorelasi menjadi satu set variabel yang tidak berkorelasi. Teknik lain yang dapat digunakan adalah regresi ridge, yang menambahkan istilah hukuman pada persamaan regresi untuk mengurangi dampak multikolinearitas pada estimasi. Dengan menangani masalah multikolinearitas, kita dapat memastikan bahwa analisis regresi menghasilkan hasil yang akurat dan dapat diandalkan tanpa memengaruhi makna data yang terkandung dalam dokumen ini.
Tidak Ada Autokorelasi (untuk data deret waktu)
Asumsi keenam dari analisis regresi adalah tidak adanya autokorelasi. Autokorelasi mengacu pada situasi di mana residual berkorelasi satu sama lain. Ini berarti bahwa kesalahan dalam model tidak independen satu sama lain, yang dapat menyebabkan estimasi bias, inferensi yang salah, dan prediksi yang buruk.
Untuk memeriksa autokorelasi, kita dapat menggunakan plot residual atau uji Durbin-Watson. Jika terdeteksi adanya autokorelasi, maka dapat menggunakan teknik seperti analisis deret waktu atau kuadrat terkecil yang umum untuk menangani asumsi tersebut.
Misalnya, analisis deret waktu adalah teknik statistik yang digunakan untuk menganalisis data berbasis waktu. Ini dapat digunakan untuk memodelkan struktur data deret waktu dan mengidentifikasi pola dan tren. Kuadrat terkecil yang umum, di sisi lain, adalah metode analisis regresi yang digunakan untuk menangani data yang memiliki kesalahan yang berkorelasi. Ini bekerja dengan menggunakan matriks kovariansi untuk memodelkan hubungan antara kesalahan. Dengan menggunakan teknik ini, kita dapat secara efektif menangani asumsi tidak adanya autokorelasi dan meningkatkan akurasi model regresi.


